[This is the third part of a four part essay–here is Part I.]
If we are going to develop an Artificial Intelligence system as good as a human, an ECW or SLP say, from Part II of this essay, and if we want to get beyond that, we need to understand what current AI can hardly do at all. That will tell us where we need to put research effort, and where that will lead to progress towards our Super Intelligence.
The seven capabilities that I have selected below start out as concrete, but get fuzzier and fuzzier and more speculative as we proceed. It is relatively easy to see the things that are close to where we are today and can be recognized as things we need to work on. When those problems get more and more solved we will be living in different intellectual world than we do today, dependent on the outcomes of that early work. So we can only speak with conviction about the short term problems where we might make progress.
And by short term, I mean the things we have already been working on for forty plus years, sometimes sixty years already.
And there are lots of other things in AI that are equally hard to do today. I just chose seven to give some range to my assertion that there is lots to do.
1. Real perception
Deep Learning brought fantastic advances to image labeling. Many people seem to think that computer vision is now a solved problem. But that is nowhere near the truth.
Below is a picture of Senator Tom Carper, ranking member of the U.S. Senate Committee on Environment and Public Works, at a committee hearing held on the morning of Wednesday June 13th, 2018, concerning the effect of emerging autonomous driving technologies on America’s roads and bridges.

He is showing what is now a well known particular failure of a particular Deep Learning trained vision system for an autonomous car. The stop sign in the left has a few carefully placed marks on it, made from white and black tape. The system no longer identifies it as a stop sign, but instead thinks that is a forty five mile per hour speed limit sign. If you squint enough you can sort of see the essence of a “4” at the bottom of the “S” and the “T”, and sort of see the essence of a “5” at the bottom of the “O” and the “P”.
But really how could a vision system that is good enough to drive a car around some of the time ever get this so wrong? Stop signs are red! Speed limit signs are not red. Surely it can see the difference between signs that are red and signs that are not red?
Well, no. We think redness of a stop sign is an obvious salient feature because our vision systems have evolved to be able to detect color constancy. Under different lighting conditions the same object in the world reflects different colored light–if we just zoom in on a pixel of something that “is red”, it may not have a red value in the image from the camera. Instead our vision system uses all sorts of cues, including detecting shadows, knowing things about what color a particular object “should” be, and local geometric relationships between measured colors in order for our brain to come up with a “detected color”. This may be very different from the color that we get from simply looking at the red/green/blue values of pixels in a camera image.
The data sets that are used to train Deep Learning systems do not have detailed color labels for little patches of the image. And the computations for color constancy are quite complex, so they are not something that the Deep Learning systems simply stumble upon.
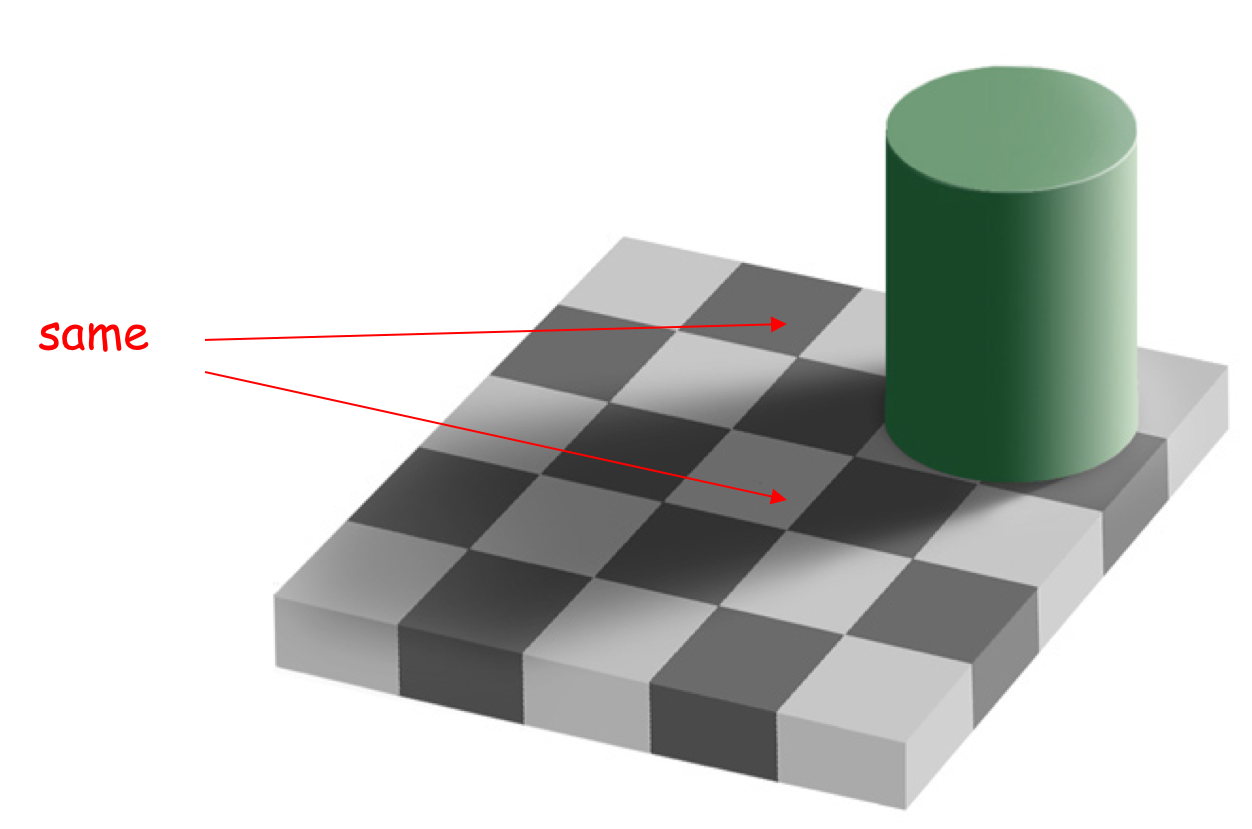
Look at the synthetic image of a  checker below, produced by Professor Ted Adelson at MIT. We can see it is and say it is a checkerboard because it is made up of squares that alternate between black and white, or at least relatively darker and lighter. But wait, they are not squares in the image at all. They are squished. Our brain is extracting three dimensional structure from this two dimensional image, and guessing that it is really a flat plane of squares that is at a non-orthogonal angle to our line of sight–that explains the consistent pattern of squishing we see. But wait, there is more. Look closely at the two squished squares that are marked “same” in this image. One is surely black and one is surely white. Our brains will not let us see the truth, however, so I have done it for your brain.
checker below, produced by Professor Ted Adelson at MIT. We can see it is and say it is a checkerboard because it is made up of squares that alternate between black and white, or at least relatively darker and lighter. But wait, they are not squares in the image at all. They are squished. Our brain is extracting three dimensional structure from this two dimensional image, and guessing that it is really a flat plane of squares that is at a non-orthogonal angle to our line of sight–that explains the consistent pattern of squishing we see. But wait, there is more. Look closely at the two squished squares that are marked “same” in this image. One is surely black and one is surely white. Our brains will not let us see the truth, however, so I have done it for your brain.
Here I grabbed a little piece of image from the top (black) square on the left and the bottom (white) square in the middle.



In isolation neither is clearly black nor white. Our vision system sees a shadow being cast by the green cylinder and so lightens up our perception of the one we see as a white square. And it is surrounded by even darker pixels in the shadowed black squares, so that adds to the effect. The third patch above is from the black square between the two labeled as the same and is from the part of that square which falls in the shadow. If you still don’t believe me print out the image and then cover up all but the regions inside the two squares in question. They will then pop into being the same shade of grey.
For more examples like this see the blue (but red) strawberries from my post last year on what is it like to be a robot?.
This is just one of perhaps a hundred little (or big) tricks that our perceptual system has built for us over evolutionary time scales. Another one is extracting prosody from people’s voices, compensating automatically for background noise, our personal knowledge of that person and their speech patterns, and more generally from simply knowing their gender, age, what their native language is, and perhaps knowing where they grew up. It is effortless for us, but it is something that lets us operate in the world with other people, and limits the extent of our stupid social errors. Another is how we are able to estimate space from sound, even when listening over a monaural telephone channel–we can tell when someone is in a large empty building, when they are outside, when they are driving, when they are in wind, just from qualities of the sound as they speak. Yet another is how we can effortlessly recognize people a from picture of their face, less than 32 pixels on a side, including often a younger version of them that we never met, nor have seen in photos before. We are incredibly good at recognizing faces, and despite recent advances we are still better than our programs. The list goes on.
Until ECW and SLP have the same hundred or so tricks up their sleeves they are not going to understand the world in the way that we do, and that will be critically important as they are not going to be able to relate to our world in the way that we do, and so neither of them will be able to do their assigned tasks. They will come off as blatant doofuses. When doddering Rodney, struggling for a noun that he can’t retrieve, says to ECW “That red one, over there!” it will not do ECW much good unless it can map red to something that may not appear red at all in terms of pixels.
2. Real Manipulation
I can reach my hand into my pants pocket and pull out my car keys blindly and effortlessly. I am not letting a robot near my pants pocket any time soon.
Dexterous manipulation has turned out to be fiendishly hard, and making dexterous hands no easier. People always ask me what would it take to make significant progress. If I knew that I would have tried it long ago.
Soon after I arrived at the Stanford Artificial Intelligence Laboratory in 1977 I started programming a couple of robot arms. Below is a picture of the “Gold Arm”, one of the two that I programmed, in a display case at one of the entrances to the Computer Science Department building at Stanford. Notice the “hand”, parallel fingers that slide together and apart. That was all we had for hands back then.
And below is a robot hand that my company was selling forty years later, in 2017. It is the same fundamental mechanical design (a ball screw moving the two fingers of a parallel jaw gripper together and apart, with some soft material on the inside of the fingers (it has fallen off one finger in the 1977 robot above)). That is all we have now. Not much has happened practically with robot hands for the last four decades.

Beyond that, however, we can not make our robot hands perform anywhere near the tasks that a human can do. In fulfillment centers, the places that pack our orders for online commerce, the movement to a single location of all the items to be packed for a given order has been largely solved. Robots bring shelves full of different items to one location. But then a human has to pick the correct item off of each shelf, and a human has to pack them into a shipping box, deciding what packing material makes sense for the particular order. The picking and packing has not been solved by automation. Despite the fact that there is economic motivation, as there was for turning lead into gold, that is pushing lots of research into this area.
Even more so the problem of manipulating floppy materials, like fabrics for apparel manufacture, or meat to be carved, or humans to be put to bed, has had very little progress. Our robots just can not do this stuff. That is alright for SLP but a big problem for ECW.
By the way, I always grimace when I see a new robot hand being showed off by researchers, and rather than being on the end of a robot arm, the wrist of the robot hand is in the hands of a human who is moving the robot hand around. You have probably used a reach grabber, or seen someone else use one. Here is a random image of one that I grabbed (with my mouse!) off an e-commerce website:

If you have played around with one of these, with its simple plastic two fingers and only one grasping motion, you will have been much more dexterous than any robot hand in the history of robotics. So even with this simple gripper, and a human brain behind it, and with no sense of touch on the distal fingers, we get to see how far off we are with robot grasping and manipulation.
3. Read a Book
Humans communicate skills and knowledge through books and more recently through “how to” videos. Although you will find recent claims that various “robots”, or AI systems can learn from a video or from reading a book, none of these demonstrations have the level of capability of a child, and the approaches people are taking are not likely to generalize to human level competence. We will come back to this point shortly.
But in the meantime, here is what an AI system would need to be able to do if it were to have human level competence at reading books in general. Or truly learn skills from watching a video.
Books are not written as mathematical proofs where all the steps are included. Actually mathematical proofs are not written that way either. We humans fill in countless steps as we read, incorporating our background knowledge into the understanding process.
Why does this work? It is because humans wrote the books and implicitly know what background information all human readers will have. So they write with the assumption that they understand what the humans reading the book will have as background knowledge. So surely an AI system reading a book will need to have that same background.
“Hold on”, the machine learning “airplanes not birds” fanboys say! We should expect Super Intelligences to read books written for Super Intelligences, not those ones written for measly humans. But that claim, of course, has two problems. First, if it really is a Super Intelligence it should be able to understand what mere humans can understand. Second, we need to get there from here, so somehow we are going to have to bootstrap our Super progeny, and the ones writing the books for the really Super ones will first need to learn from books written for measly humans.
But now, back to this background knowledge. It is what we all know about the world and can expect one another to know about the world. For instance, I don’t feel the need to explain to you right now, dear reader, that the universe of intelligent readers and discussants of ideas on Earth at this moment are all members of the biological species Homo Sapiens. I figure you already know that.
This could be called “common sense” knowledge. It is necessary for so much of our (us humans) understanding of the world, and it is an assumed background in all communications between humans. Not only that, it is an enabler of how we make plans of action.
Two NYU professors, Ernest Davis (computer science) and Gary Marcus (psychology and neural science) have recently been highlighting just how much humans rely on common sense to understand the world, and what is missing from computers. Besides their recent opinion piece in the New York Times on Google Duplex they also had a long article2 about common sense in a popular computer science magazine. Here is the abstract:
Who is taller, Prince William or his baby son Prince George? Can you make a salad out of a polyester shirt? If you stick a pin into a carrot, does it make a hole in the carrot or in the pin? These types of questions may seem silly, but many intelligent tasks, such as understanding texts, computer vision, planning, and scientific reasoning require the same kinds of real-world knowledge and reasoning abilities. For instance, if you see a six-foot-tall person holding a two-foot-tall person in his arms, and you are told they are father and son, you do not have to ask which is which. If you need to make a salad for dinner and are out of lettuce, you do not waste time considering improvising by taking a shirt out of the closet and cutting it up. If you read the text, “I stuck a pin in a carrot; when I pulled the pin out, it had a hole,” you need not consider the possibility “it” refers to the pin.
As they point out, so called “common sense” is important for even the most mundane tasks we wish our AI systems to do for us. They enable both Google and Bing to do this translation: “The telephone is working. The electrician is working.” in English, becomes “Das Telefon funktioniert. Der Elektriker arbeitet.” in German. The two meanings of “working” in English need to be handled differently in German, and an electrician works in one sense, whereas a telephone works in another sense. Without this common sense, somehow embedded in an AI system, it is not going to be able to truly understand a book. But this example is only a tiny one step version of common sense.
Correctly translating even 20 or 30 words can require a complex composition of little common sense atoms. Douglas Hofstadter pointed out in a recent Atlantic article places where things in short order can get just too complicated for Google translate, despite deep learning have enabled the process. In his examples it is context over many sentences that get the systems into trouble. Humans handle these cases effortlessly. Even four years olds (see Part IV of this post).
He says, when comparing how he translates to how Google translates:
Google Translate is all about bypassing or circumventing the act of understanding language.
…
I am not, in short, moving straight from words and phrases in Language A to words and phrases in Language B. Instead, I am unconsciously conjuring up images, scenes, and ideas, dredging up experiences I myself have had (or have read about, or seen in movies, or heard from friends), and only when this nonverbal, imagistic, experiential, mental “halo” has been realized—only when the elusive bubble of meaning is floating in my brain—do I start the process of formulating words and phrases in the target language, and then revising, revising, and revising.
In the second paragraph he touches on the idea of gaining meaning from running simulations of scenes in his head. We will come back to this in the next item of hardness for AI. And elsewhere in the article he even points out how when he is translating he uses Google search, a compositional method that Google translate does not have access to.
Common sense lets a program, or a human, prune away irrelevant considerations. A program may be able to exhaustively come up with many many options about what a phrase or a situation could mean, all the realms of possibility. What common sense can do is quickly reduce that large set to a much smaller set of plausibility, and beyond that narrow things down to those cases with significant probability. From possibility to plausibility to probability. When my kids were young they used to love to tease dad by arguing for possibilities as explanations for what was happening in the world, and tie me into knots as I tried to push back with plausibilities and probabilities. It was a great game.
This common sense has been a a long standing goal for symbolic artificial intelligence. Recently the more rabid Deep Learners have claimed that their systems are able to learn aspects of common sense, and that is sometimes a little bit true. But unfortunately it does not come out in a way that is compositional–it usually requires a human to interpret the result of an image or a little movie that the network generates in order for the researchers to demonstrate that it is common sense. The onus, once again is on the human interpreter. Without composition, it is not likely to be as useful or as robust as the human capabilities we see in quite small children.
The point here that simply reading a book is very hard, and requires a lot of what many people have called “common sense”. How that common sense should be engendered in our AI systems is a complex question that we will return to in Part IV.
Now back to claims that we already have AI systems that can read books.
Not too long ago an AI program outperformed MIT undergraduates on the exam for Freshman calculus. Some might think that that means that soon AI programs will be doing better on more and more classes at MIT and that before too long we’ll have an AI program fulfilling the degree requirements at MIT. I am confident that it will take more than fifty years. Supremely confident, and not just because an MIT undergraduate degree requires that each student pass a swimming test. No, I am supremely confident on that time scale because the program, written by Jim Slagle1 for his PhD thesis with Marvin Minsky, outperformed MIT students in 1961. 1961! That is fifty seven years ago already. Mainframe computers back then were way less than what we have now in programmable light switches or in our car key frob. But an AI program could beat MIT undergraduates at calculus back then.
When you see an AI program touted as having done well on a Japanese college entrance exam, or passing a US 8th grade science test, please do not think that the AI is anywhere near human level and going to plow through the next few tests. Again this is one of the seven deadly sins of mistaking performance on a narrow task, taking the test, for competence at a general level. A human who passes those tests does it in a human way that means that they have a general competence around the topics in the test. The test was designed for humans and inherent in the way it is designed it extracts information about the competence of a human who took the test. And the test designers did not even have to think about it that way. It is just they way they know how to design tests. (Although we have seen how “teaching to the test” degrades that certainty even for human students, which is why any human testing regime eventually needs to get updated or changed completely.) But that test is not testing the same thing for an AI system. Just like a stop sign with a few pieces of tape on it may not look at all like a stop sign to a Deep Learning system that is supposed to drive your car.
At the same time the researchers, and their institutional press offices, are committing another of the seven deadly sins. They are trying to demonstrate that there system is able to “read” or “understand” by demonstrating preformance on a human test (despite my argument above that the tests are not valid for machines), and then they claim victory and let the press grossly overgeneralize.
4. Diagnose and Repair Stuff
If ECW is going to be a useful elder care robot in a home it out to be able to figure out when something has gone wrong with the house. At the very least it should be able to know which specialist to call to come and fix it. If all it can do is say “something is wrong, something is wrong, I don’t know what”, we will hardly think of it as Super Intelligent. At the very least it should be able to notice that the toilet is not flushing so the toilet repair person should be called. Or that a light bulb is out so that the handy person should be called. Or that there is no electricity at all in the house so that should be reported to the power company.
We have no robots that could begin to do these simple diagnosis tasks. In fact I don’t know of any robot that would realize when the roof had blown off a house that they were in and be able to report that fact. At best today we could expect a robot to detect that environmental conditions were anomalous and shut themselves down. But in reality I think it is more likely that they would continue trying to operate (as a Roomba might after it has run over a dog turd with its rapidly spinning brushes–bad…) and fail spectacularly.
But more than what we referred to as common sense in the previous section, it seems that when humans diagnose even simply problems they are running some sort of simulation of the world in their heads, looking at possibilities, plausibilities, and probabilities. It is not exact the 3D accurate models that traditional robotics uses to predict the forces that will be felt as a robot arm moves along a particular trajectory (and thereby notice when it has hit something unexpected and the predictions are not borne out by the sensors). It is much sloppier than that, although geometry may often be involved. And it is not the simulation as a 2D movie that some recent papers in Deep Learning suggest is the key, but instead is very compositional across domains. And it often uses metaphor. This simulation capability will be essential for ECW to provide full services as a trusted guardian of the home environment for an elderly person. And SLP will need such generic simulations to check out how its design for people flow will work in its design of the dialysis ward.
Again, our AI systems and robots may not have to do things exactly the way we do them, but they will need to have the same general competence as, or more than, humans if we are going to think of them as being as smart as us.
Right now there are really no systems that have either common sense or this general purpose simulation capability. That is not to say that people have not worked on these problems for a long long time. I was very impressed by a paper on this topic at the very first AI conference I ever went to, IJCAI 77 held at MIT in August 1977. The paper was by Brian Funt, and was WHISPER: A Problem-Solving System Utilizing Diagrams and a Parallel Processing Retina. Funt was a post doc at Stanford with John McCarthy, the namer of Artificial Intelligence and the instigator of the foundational 1956 workshop at Dartmouth. And McCarthy’s first paper on “Programs with Common Sense” was written in 1958. We have known these problems are important for a long long time. People have made lots of worthwhile progress on them over the last few decades.They still remain hard and unsolved and not read for prime time deployment in real products.
“But wait”, you say. You have seen a news release about a robot building a piece of IKEA furniture. Surely that requires common sense and this general purpose simulation. Surely it is already solved and Super Intelligence is right around the corner. Again, don’t hold your breath–fifty years is a long time for a human to go without oxygen. When you see such a demo it is with a robot and a program that has been worked on by many graduate students for many months. The pieces were removed from the boxes by the graduate students (months ago). They have run the programs again, and again, and again, and finally may have one run where it puts some parts of the furniture together. The students were all there, all making sure everything went perfectly. This is completely different from what we might expect from ECW, taking delivery of some IKEA boxes at the door, carrying them inside (with no graduate students present), opening the boxes and taking out the famous IKEA instructions and reading them. And then putting the furniture together.
It would be very helpful if ECW could do these things. Any robot today put in this situation will fail dismally on many of the following steps (and remember, this is a robot in a house that the researchers have never seen).
- realizing there is a delivery being made at the house
- getting the stuff up any steps and inside
- actually opening the boxes without knowing exactly what is inside and without damaging the parts
- finding the instructions, and manipulating the paper to see each side of each page
- understanding the instructions
- planning out where to place the pieces so that they are available in the right order
- manipulating two or three pieces at once when they need to be joined
- finding and retrieving the right tools (screwdrivers, hammers to tap in wooden dowels)
- doing that finely skilled manipulation
Not one of these subtasks can today be done by a robot in some unknown house with a never before seen piece of IKEA furniture, and without a team of graduate students having worked for month on the particular instance of that subtask in the particular environment.
When academic researchers say they have solved a problem, or demonstrated a robot capability that is a long long way from the level of performance we will expect from ECW.
Here is a little part of a short paper that just came out3 in the AAAI’s (Association for the Advancement of Artificial Intelligence) AI Magazine this summer, written by Alexander Kleiner about his transition from being an AI professor to working in AI systems that had to work in the real world, every day, every time.
After I left academe in 2014, I joined the technical organization at iRobot. I quickly learned how challenging it is to build deliberative robotic systems exposed to millions of individual homes. In contrast, the research results presented in papers (including mine) were mostly limited to a handful of environments that served as a proof of concept.
Academic demonstrations are important steps towards solving these problems. But they are demonstrations only. Brian Funt demonstrated a program that could imagine the future few seconds, forty one years ago, before computer graphics existed (his 1977 paper uses line printer output of fixed width characters to produce diagrams). That was a good early step. But despite the decades of hard work we are still not there yet, by a long way.
5. Relating Human and Robot Behavior to Maps
As I pointed out in my what is it like to be a robot? post, our home robots will be able to have a much richer set of sensors than we do. For instance they can have built in GPS, listen for Bluetooth and Wifi, and measure people’s breathing and heartbeat a room away4 by looking for subtle changes in Wifi signals propagating through the air.
Our self-driving cars (such as they are really self driving yet) rely heavily on GPS for navigation. But GPS now gets spoofed as a method of attack, and worse, some players may decide to bring down one of more GPS satellites in a state sponsored act of terrorism.
Things will be really bad for a while if GPS goes down. For one thing the electrical grid will need to be partitioned into much more local supplies as GPS is used to synchronize the phase of AC current in distant parts of the network. And humans will be lost quite a bit until paper maps once again get printed for all sorts of applications. E-commerce deliveries will be particularly badly hit for a while, as well as flight and boat navigation (early 747’s had a window in the roof of the cockpit for celestial navigation across the Pacific; the US Naval Academy brought back into its curriculum navigation by the stars in 2016).
Whether it is spoofing, an attack on satellites, or just lousy reception, we would hope that our elder care robots, our ECWs, are not taken offline. They will be, unless they get much better at visual and other navigation without relying at all on hints from GPS. This will also enable them to work in rapidly changing environments where maps may not be consistent from one day to the next, nor necessarily be available.
But this is just the start. Maps, including terrain and 3D details will be vital for ECW to be able to decide where it can get its owner to walk, travel in a wheel chair, or move within a bathroom. This capability is not so hard for current traditional robotics approaches. But for SLP, the Services Logistics Planner, it will need to be a lot more generic. It will need to relate 3D maps that it builds in its plans for a dialysis ward to how a hypothetical human patient, or a group of hypothetical staff and patients, will together and apart navigate around the planned environment. It will need to build simulations, by itself, with no human input, of how groups of humans might operate.
This capability, of projecting actions through imagined physical spaces is not too far off from what happens in video games. It does not seem as far away as all the other items in this blog post. It still requires some years of hard work to make systems which are robust, and which can be used with no human priming–that part is far away from any current academic demonstrations.
Furthermore, being able to run such simulations will probably contribute to aspects of “common sense”, but it all has to be much more compositional than the current graphics of video games, and much more able to run with both plausibility and probability, rather than just possibility.
This is not unlike the previous section on diagnosis and repair, and indeed there is much commonality. But here we are pushing deeper on relating the three dimensional aspects of the simulation to reality in the world. For ECW it will the actual world as it is. For SLP it will be the world as it is designing it, for the future dialysis ward, and constraints will need to flow in both directions so that after a simulation, the failures to meet specifications or desired outcomes can be fed back into the system.
6.Write Or Debug a Computer Program
OK, I admit I am having a little fun with this section, although it is illustrative of human capabilities and forms of intelligence. But feel free to skip it, it is long and a little technical.
Some of the alarmists about Super Intelligence worry that when we have it, it will be able to improve itself by rewriting its own code. And then it will exponentially grow smarter than us, and so, naturally, it will kill us all. I admit to finding that last part perplexing, but be that as it may.
You may have seen headlines like “Learning Software Learns to Write Learning Software”. No it doesn’t. In this particular case there was a fixed human written algorithm that went through a process of building a particular form of Deep Learning network. And a learning network that learned how to adjust the parameters of that algorithm which ended up determining the size, connectivity, and number of layers. It didn’t write a single line of computer code.
So, how do we find our way through such a hyped up environment and how far away are we from AI systems which can read computer code, debug it, make it better, and write new computer code? Spoiler alert: about as far away as it is possible to be, like not even in the same galaxy, let alone as close as orbiting hundreds of millions of miles apart in the same solar system.
Each of today’s AI systems are many millions of lines of code, they have been written by many, many, people through shared libraries, along with, for companies delivering AI based systems, perhaps a few million lines of custom and private code bases. They usually span many languages such as C, C++, Python, Javascript, Java, and others. The languages used often have only informal specifications, and in the last few years new languages have been introduced with alarming frequency and different versions of the languages have different semantics. It’s all a bit of a mess, to everyone except the programmers whose lives these details are.
On top of this we have known since Turing introduced the halting problem in 1936 that it is not possible for computers to know certain rather straightforward things about how any given program might perform over all possible inputs. In 1967 Minsky warned that even for computers with relatively small amounts of memory (about what we expect in a current car key frob) that to figure out some things about their programs would take longer then the life of the Universe, even with all the Universe doing the computing in parallel.
Humans are able to write programs with some small amount of assuredness that they will work by using heuristics in analyzing what the program might do. They use various models and experiments and mental simulations to prove to themselves that their program is doing what they want. This is different from proof.
When computers were first developed we first needed computer software. We quickly went from programmers having to enter the numeric codes for each operation of the machine, to assemblers where there is a one to one correspondence between what the programmers write and that numeric code, but at least they get to write it in human readable text, like “ADD”. Then quickly after that came compilers where the language expressing the computation was at a higher level model of an abstract machine and the compiler turned that into the assembler language for any particular machine. There have been many attempts, really since the 1960s, to build AI systems which are a level above that, and can generate code in a computer language from a higher level description, in English say.
The reality is that these systems can only generate fairly generic code and have difficulty when complex logic is needed. The proponents of these systems will argue about how useful they are, but the reality is that the human doing the specifying has to move from specifying complex computer code to specifying complex mathematical relationships.
Real programmers tend to use spatial models and their “simulating the world” capabilities to reason through what code should be produced, and which cases should handled in which way. Often they will write long lists of cases, in pseudo English so that they can keep track of things, and (if the later person who is to maintain the code is lucky) put that in comments around the code. And they use variable names and procedure names that are descriptive of what is going to be computed, even though that makes no difference to the compiler. For instance they might use StringPtr for a pointer to a string, where the compiler would have been just as happy if they had used M, say. Humans use the name to give themselves a little help in remembering what is what.
People have also attempted to write AI systems to debug programs, but they rarely try to understand the variable names, and simply treat them as anonymous symbols, just as the compiler does.
An upshot of this has been “formal” programming methods which require humans to write mathematical assertions about their code, so that automated systems can have a chance at understanding it. But this is even more painful that writing computer code, and even more buggy than regular computer code, and so it is hardly ever done.
So our Super Intelligence is going to deal with existing code bases, and some of the stuff in there will be quite ugly.
Just for fun I coded up a little library routine in C–I use a library routine with the exact same semantics in another language that I regularly program in. And then I got rid of all the semantics in the variable, procedure and type names. Here is the code. It is really only one line. And, it compiles just fine using the GCC compiler and works completely correctly.
a*b(a*c) {a*d; a*e;
for(d=NULL;c!=NULL;e=(a*)*c,*c=(a)d,d=c,c=e);return d;}
I sent it to two of my colleagues who are used to groveling around in build systems and open source code in libraries, asking if they could figure out what it was. I had made it a little hard by not given them a definition of “a”.
They both figured out immediately that “a” must be a defined type. One replied that he had some clues, and started out drawing data structures and simulating the code, but then moved to experimenting by compiling it (after guessing at a definition for “a”) and writing a program that called it. He got lots of segment violations (i.e., the program kept crashing), but guessed that it was walking down a linked list. The second person said that he stared at the code and realized that “e” was a temporary variable whose use was wrapped around assignments of two others which suggested some value swapping going on. And that the end condition for the loop being when “c” became NULL, suggested to him that it was walking down a list “c”, but that list itself was getting destroyed. So he guessed it might be doing an in place list reversal, and was able to set up a simulation in his head and on paper of that and verify that it was the case.
When I gave each of them the equivalent and original form of the code with the informative names (though I admit to a little bit of old fashioned use of equivalences in the type definition) restored, along with the type definition for “a”, now called “address”, they both said it was straightforward to simulate on paper and verify what was going on.
#define address unsigned long long int
address *reverse(address *list) {
address *rev;
address *temp;
for(rev=NULL;list!=NULL;temp=(address *)*list,
*list=(address)rev,
rev=list,list=temp);
return rev;}
The reality is that variable names and comments, though irrelevant to the actual operation of code is where a lot of the semantic explanation of what is going on is encoded. Simply looking at the code itself is unlikely to give enough information about how it is used. And if you look at the total system then any sort of reasoning process about it soon becomes intractable.
If anyone had already built an AI system which could understand either of the two versions of my procedure above it would be an unbelievably useful tool for every programmer alive today. That is what makes me confident we have nothing that is close–it would be in everyone’s IDE (Integrated Development Environment) and programmer productivity would be through the roof.
But you might think my little exercise was a bit too hard for our poor Super Intelligence (the one whose proponents think will be wanting to kill us all in just a few years–poor Super Intelligence). But really you should not underestimate how badly written are the code bases on which we all rely for our daily life to proceed in an ordered way.
So I did a different, second experiment, this time just on myself.
Here is a piece of code I just found on my Macintosh, under a directory named TextEdit, in a file named EncodingManager.m. I wasn’t sure what a file extension of “.m” meant in terms of language, but it looked like C code to me. I looked only at this single procedure within that file, nothing else at all, but I can tell a few things about it, and the general system of which it is part. Note that the only words here that are predefined in C are static, int, const, void, if, and return. Everything else must be defined somewhere else in the program, but I didn’t look for the definitions, just stared at this little piece of code in isolation. I guarantee that there is no AI program today which could deduce what I did, in just a few minutes, in the italic text following the code.
/* Sort using the equivalent Mac encoding as the major key. Secondary key is the actual encoding value, which works well enough. We treat Unicode encodings as special case, putting them at top of the list.
*/
static int encodingCompare(const void *firstPtr, const void *secondPtr) {
CFStringEncoding first = *(CFStringEncoding *)firstPtr;
CFStringEncoding second = *(CFStringEncoding *)secondPtr;
CFStringEncoding macEncodingForFirst = CFStringGetMostCompatibleMacStringEncoding(first);
CFStringEncoding macEncodingForSecond = CFStringGetMostCompatibleMacStringEncoding(second);
if (first == second) return 0; // Should really never happen
if (macEncodingForFirst == kCFStringEncodingUnicode || macEncodingForSecond == kCFStringEncodingUnicode) {
if (macEncodingForSecond == macEncodingForFirst) return (first > second) ? 1 : -1; // Both Unicode; compare second order
return (macEncodingForFirst == kCFStringEncodingUnicode) ? -1 : 1; // First is Unicode
}
if ((macEncodingForFirst > macEncodingForSecond) || ((macEncodingForFirst == macEncodingForSecond) && (first > second))) return 1;
return -1;
}
First, the comment at the top is slightly misleading as this is not a sort routine, rather it is a predicate which is used by some sorting procedure to decide whether any two given elements are in the right order. It takes two arguments and returns either 1 or -1, depending on which order they should be in the sorted output from that sorting procedure which we haven’t seen yet. We have to figure out what those two possibilities mean. I know that TextEdit is a simple text file editor that runs on the Macintosh. It looks like there are a bunch of possible encodings for elements of strings inside TextEdit, and on the Macintosh there are a non-identical set of possible encodings. I’m guessing that TextEdit must run on other systems too! This particular predicate takes the encoding values for the general encodings and says which of the ones closest to each of them on the Macintosh is better to use. And it prefers encodings where only a single byte per character is used. The encodings themselves, both for the general case, and for the Macintosh are represented by an integer. Based on the third sentence in the first comment, and on the return value where the comment is “First is Unicode” it looks like this predicate returning -1 means its first argument should precede (i.e., appear closer to the “top of the list”–an inference I am making from “top” being used to refer to the end of a list that precedes all the other elements of the list; whether it is actually represented elsewhere as a classical list as in my first example of code above, or it is a sorted array is immaterial and this piece of code does not depend on that) the second argument in the sort, otherwise if it returns 1, then the second argument should precede the first argument. If the integer for the Macintosh encoding is smaller that means it should come first, and if they are equal for the Macintosh, the whether the integer representing the general case encoding is smaller should determine the order. All this subject to single byte representations always winning out.
That is a lot of things to infer about what is actually a pretty short piece of code. But it is the sort of thing that makes it so that humans can build complex systems, in the way that all our current software is built.
It is the sort of thing that any Super Intelligence bent on self improvement through code level introspection is going to need in order to understand the code that has been cobbled together by humans to produce it. Without understanding its own code it will not be able to improve itself by rewriting its own code.
And we do not have any AI system which can understand even this tiny, tiny little bit of code from a simple text editor.
7. Bond With Humans
Now we get to the really speculative place, as this sort of thing has only been worked in AI and robotics for around 25 years. Can humans interact with robots in a way in which they have true empathy for each other?
In the 1990’s my PhD student Cynthia Breazeal used to ask whether we would want the then future robots in our homes to be “an appliance or a friend”. So far they have been appliances. For Cynthia’s PhD thesis (defended in the year 2000) she built a robot, Kismet, an embodied head, that could interact with people. She tested it with lab members who were familiar with robots and with dozens of volunteers who had no previous experience with robots, and certainly not a social robot like Kismet.
I have put two videos (cameras were much lower resolution back then) from her PhD defense online.
In the first one Cynthia asked six members of our lab group to variously praise the robot, get its attention, prohibit the robot, and soothe the robot. As you can see, the robot has simple facial expressions, and head motions. Cynthia had mapped out an emotional space for the robot and had it express its emotion state with these parameters controlling how it moved its head, its ears and its eyelids. A largely independent system controlled the direction of its eyes, designed to look like human eyes, with cameras behind each retina–its gaze direction is both emotional and functional in that gaze direction determines what it can see. It also looked for people’s eyes and made eye contact when appropriate, while generally picking up on motions in its field of view, and sometimes attending to those motions, based on a model of how humans seem to do so at the preconscious level. In the video Kismet easily picks up on the somewhat exaggerated prosody in the humans’ voices, and responds appropriately.
In the second video, a naïve subject, i.e., one who had no previous knowledge of the robot, was asked to “talk to the robot”. He did not know that the robot did not understand English, but instead only detected when he was speaking along with detecting the prosody in his voice (and in fact it was much better tuned to prosody in women’s voices–you may have noticed that all the human participants in the previous video were women). Also he did not know that Kismet only uttered nonsense words made up of English language phonemes but not actual English words. Nevertheless he is able to have a somewhat coherent conversation with the robot. They take turns in speaking (as with all subjects he adjusts his delay to match the timing that Kismet needed so they would not speak over each other), and he successfully shows it his watch, in that it looks right at his watch when he says “I want to show you my watch”. It does this because instinctively he moves his hand to the center of its visual field and makes a motion towards the watch, tapping the face with his index finger. Kismet knows nothing about watches but does know to follow simple motions. Kismet also makes eye contact with him, follows his face, and when it loses his face, the subject re-engages it with a hand motion. And when he gets close to Kismet’s face and Kismet pulls back he says “Am I too close?”.
Note that when this work was done most computers only ran at about 200Mhz, a tiny fraction of what they run at today, and with only about 1,000th of the size RAM we expect on even our laptops today.
One of the key takeaways from Cynthia’s work was that with just a few simple behaviors the robot was able to engage humans in human like interactions. At the time this was the antithesis of symbolic Artificial Intelligence which took the view that speech between humans was based on “speech acts” where one speaker is trying to convey meaning to another. That is the model that Amazon Echo and Google Home use today. Here it seemed that social interaction, involving speech was built on top of lower level cues on interaction. And furthermore that a human would engage with a physical robot if there were some simple and consistent cues given by the robot.
This was definitely a behavior-based approach to human speech interaction.
But is it possible to get beyond this? Are the studies correct that try to show an embodied robot is engaged with better by people than a disembodied graphics image, or a listening/speaking cylinder in the corner of the room?
Let’s look at the interspecies interaction that people engage in more than any others.

This photo was in a commentary in the issue of Science that published a paper5 by Nagasawa et al, in 2015. The authors show that as oxytocin concentration rises for whatever reason in a dog or its owner then the one with the newly higher level engages more in making eye contact. And then the oxytocin level in the other individual (dog or human) rises. They get into a positive feedback loop of oxytocin levels mediated by the external behavior of each in making sustained eye contact.
Cynthia Breazeal did not monitor the oxytocin levels in her human subjects as they made sustained eye contact with Kismet, but even without measuring it I am quite sure that the oxytocin level did not rise in the robot. The authors of the dog paper suggest that in their evolution, while domesticated, dogs stumbled upon a way to hijack an interaction pattern that is important for human nurturing of their young.
So, robots, and Kismet was a good start, could certainly be made to hijack that same pathway and perhaps others. It is not how cute they look, nor how similar they look to a human, Kismet is very clearly non-human, it is how easy it is to map their behaviors to ones for which us humans are primed.
Now here is a wacky thought. Over the last few years we have learned how many species of bacteria we carry in out gut (our micro biome), on our skin, and in our mouths. Recent studies suggest all sorts of effects of just what bacterial species we have and how that influences and is influenced by sexual attraction and even non-sexual social compatibility. And there is evidence of transfer of bacterial species between people. What if part of our attraction to dogs is related to or moderated by transfer of bacteria between us and them? We do not yet know if it is the case. But if it is that may doom our social relationships with robots from ever becoming as strong as with dogs. Or people. At least, that is, until we start producing biological replicants as our robots, and by then we will have plenty of other moral pickles to deal with.
With that, we move to the next installment of our quest to build Super Intelligence, Part IV, things to work on now.
1 “A Heuristic Program that Solves Symbolic Integration Problems in Freshman Calculus”, James R. Slagle, in Computers and Thought, Edward A. Feigenbaum and Julian Feldman, McGraw-Hill , New York, NY, 1963, 191–206, adapted from his 1961 PhD thesis in mathematics at MIT.
2 “Commonsense Reasoning and Commonsense Knowledge in Artificial Intelligence”, Ernest Davis and Gary Marcus, Communications of the ACM, (58)9, September 2015, 92–103.
3 “The Low-Cost Evolution of AI in Domestic Floor Cleaning Robots”, Alexander Kleiner, AI Magazine, Summer 2018, 89–90.
4 See Dina Katabi’s recent TED talk from 2018.
5 “Oxytocin-gaze positive loop and the coevolution of human-dog bonds”, Miho Nagasawa, Shouhei Mitsui, Shiori En, Nobuyo Ohtani, Mitsuaki Ohta,Yasuo Sakuma, Tatsushi Onaka, Kazutaka Mogi, and Takefumi Kikusui, Science, volume 343, 17th April, 2015, 333–336.